概率趣题——吃豆子

按

这篇文章是我在知乎上看到的概率题目后，自己分析、解答的过程。从简单程序模拟入手，到递推式和动态规划，最后求出解析解并证明。希望能给你带来启发。

题目

袋子中有白色、黑色两种豆子，且数量相等。每次进行如下操作：

• 从袋子中随机抽取一颗豆子；
• 若为黑色，则直接吃掉；
• 若为白色，则放回重新随机抽取一次，然后不论是什么颜色都直接吃掉。

重复上述操作直到袋中没有豆子。求最后一颗被吃掉的豆子是黑色的概率。

题目分析

显然黑色豆子更有可能被吃掉，所以袋中的白色豆子所占比例应该趋向于越来越大。所以最终所求概率应该小于$\frac{1}{2}$。

假设初始有$n$个白色豆子和$n$个黑色豆子。当$n=1$时，我们可以计算出概率：

$$P(\text{最后一颗是黑色})=P(\text{第一次抽到白色})\ast P(\text{第二次抽到白色})=\frac{1}{4}$$

当$n$变大时，所求概率会更小。因为随着操作次数的增多，黑色豆子应该越来越少，直到达到某个比例，使得黑色豆子被抽出吃掉的概率和白色豆子相等，这样二者的比例才会稳定。随着$n\to \infty$，这个比例应该也逐渐趋近于$0$。那么所求概率也应该逐渐趋近于$0$。

让我们写个程序看看推测是否正确。

编程模拟

设最后一个被吃掉的豆子是黑色的概率为$P(n)$，其中$n$是初始时白色豆子的数量和黑色豆子的数量。

首先让我们验证$P(1)=\frac{1}{4}$。

import random
from typing import Tuple

# 用 Tuple[int, int] 描述容器状态（白色豆子数，黑色豆子数）
ContainerState = Tuple[int, int]

# 操作一次（指按题目操作直到吃掉一颗豆子），并返回容器状态
def operate_once(state: ContainerState) -> ContainerState:
    selection = 0 if random.randint(0, state[0] + state[1] - 1) < state[0] else 1
    if selection == 0:
        # 抽到白色豆子，放回并重新抽取
        selection = 0 if random.randint(0, state[0] + state[1] - 1) < state[0] else 1
    if selection == 0:
        return state[0] - 1, state[1]
    else:
        return state[0], state[1] - 1

# 模拟一遍完整的操作过程，并返回最后一个吃掉的豆子的颜色（0 为白色，1 为黑色）
def simulate(n: int) -> int:
    state = n, n
    while state[0] and state[1]:
        state = operate_once(state)
    return 0 if state[0] else 1

# 模拟多次，并计算 P(n)；其中 T 为总模拟次数
def simulate_and_calc_prob(n: int, T: int = 100000) -> float:
    num_cases_last_is_black = 0
    num_cases_total = T
    for _ in range(num_cases_total):
        result = simulate(n)
        if result == 1:
            num_cases_last_is_black += 1
    return float(num_cases_last_is_black) / float(num_cases_total)

print("P(1) =", simulate_and_calc_prob(1))

P(1) = 0.25098

更多的豆子

结果和我们预想的一致。让我们尝试一下更大的$n$。

for n in [1, 2, 3, 4, 5, 10, 100]:
    print("P({}) =".format(n), simulate_and_calc_prob(n))

P(1) = 0.25073
P(2) = 0.16579
P(3) = 0.12502
P(4) = 0.09817
P(5) = 0.08408
P(10) = 0.04548
P(100) = 0.005

更快的程序？

好吧，结果确实随着$n$的增大而逐渐接近零了，这符合我们的预期。但是这个程序太慢了，我们来尝试加速一下这个程序。

注意到每次抽取豆子时，抽到不同豆子的概率与剩余两种豆子的数量有关。假设现在有$x$个白色豆子和$y$个黑色豆子，下一个吃掉的豆子的颜色为白色和黑色的概率分别是：

$$\begin{array}{rl}P(\text{吃到白色豆子})& =P(\text{第一次抽出白色})\cdot P(\text{第二次抽出白色})\\ & =\frac{x}{x+y}\times \frac{x}{x+y}\\ & =\frac{x^2}{(x+y{)}^2}\\ P(\text{吃到黑色豆子})& =P(\text{第一次抽到黑色})+P(\text{第一次抽到白色})\cdot P(\text{第二次抽到黑色})\\ & =\frac{y}{x+y}+\frac{x}{x+y}\times \frac{y}{x+y}\\ & =\frac{2xy+y^2}{(x+y{)}^2}\end{array}$$

让我们基于这些公式重写一下程序。

# 操作一次（指按题目操作直到吃掉一颗豆子），并返回容器状态
def operate_once_faster(state: ContainerState) -> ContainerState:
    prob_white = float(state[0]) * float(state[0]) / (float(state[0] + state[1]) * float(state[0] + state[1]))
    selection = 0 if random.random() < prob_white else 1
    if selection == 0:
        return state[0] - 1, state[1]
    else:
        return state[0], state[1] - 1
    
# 模拟一遍完整的操作过程，并返回最后一个吃掉的豆子的颜色（0 为白色，1 为黑色）
def simulate_faster(n: int) -> int:
    state = n, n
    while state[0] and state[1]:
        state = operate_once_faster(state)
    return 0 if state[0] else 1

# 模拟多次，并计算 P(n)；其中 T 为总模拟次数
def simulate_and_calc_prob_faster(n: int, T: int = 100000) -> float:
    num_cases_last_is_black = 0
    num_cases_total = T
    for _ in range(num_cases_total):
        result = simulate_faster(n)
        if result == 1:
            num_cases_last_is_black += 1
    return float(num_cases_last_is_black) / float(num_cases_total)

for n in [1, 2, 3, 4, 5, 10, 100]:
    print("P({}) =".format(n), simulate_and_calc_prob_faster(n))

P(1) = 0.25076
P(2) = 0.1669
P(3) = 0.1241
P(4) = 0.10211
P(5) = 0.08278
P(10) = 0.04681
P(100) = 0.00507

不再模拟

当然刚才这样并不会让程序变快，因为总的模拟次数并没有变少。（虽然我们调用random()函数的次数确实变少了。）但观察这些公式，我们可以发现一个不用多次模拟就能求得概率的方法！

设当前状态为$(x,y)$，即有$x$颗白色豆子和$y$颗黑色豆子。我们用$P(x,y)$表示$P(\text{最后一颗是黑色}|\text{状态为}(x,y))$。那么$P(n,n)$就是题目所求概率。注意：我们之所以可以这样做，是因为在状态为$(x,y)$的情况下，最后一颗是黑色的概率与之前的豆子数、吃豆顺序都已经无关了，即我们常说的“无后效性”。

利用递推的方法，我们可以建立$P(x,y)$和$P(x-1,y)$、$P(x,y-1)$之间的关系：

$$\begin{array}{rl}P(x,y)& =P(\text{吃到白色豆子})\cdot P(x-1,y)+P(\text{吃到黑色豆子})\cdot P(x,y-1)\\ & =\frac{x^2}{(x+y{)}^2}\cdot P(x-1,y)+\frac{2xy+y^2}{(x+y{)}^2}\cdot P(x,y-1)\end{array}$$

我们还知道初始条件：

$$\begin{array}{rl}P(0,y)& =1\\ P(x,0)& =0\end{array}$$

那么我们可以用动态规划的方法求出$P(n,n)$的值。

from typing import List

# 用动态规划计算 P(x, y)
def calc_prob_by_dp(n: int) -> float:
    # p[x] = P(x, y)，其中 y 随着迭代的进行会不断变化。
    p: List[float] = [0.0] * (n + 1)
    # last_p[x] = P(x, y - 1)
    last_p: List[float] = [0.0] * (n + 1)
    
    for y in range(1, n + 1):
        p[0] = 1.0
        for x in range(1, n + 1):
            prob_white = float(x) * float(x) / (float(x + y) * float(x + y))
            p[x] = prob_white * p[x - 1] + (1.0 - prob_white) * last_p[x]
        p, last_p = last_p, p
    
    return last_p[n]

for n in [1, 2, 3, 4, 5, 10, 100]:
    print("P({}) =".format(n), calc_prob_by_dp(n))

P(1) = 0.25
P(2) = 0.16666666666666666
P(3) = 0.125
P(4) = 0.09999999999999999
P(5) = 0.08333333333333333
P(10) = 0.04545454545454545
P(100) = 0.004950495049504951

画图

虽然得到了数值解，但是我们感觉到，这个题目应该是有解析解的，解析解可以通过递推式求出。但是我这么菜，显然是看不出来如何求解析解的，所以我们从数值解找找规律。

我们来画一下$P(n,n)$随$n$变化的图像。

# 用动态规划计算 P(x, y)
def calc_prob_by_dp_all(n: int) -> List[float]:
    # p[x] = P(x, y)，其中 y 随着迭代的进行会不断变化。
    p: List[float] = [0.0] * (n + 1)
    # last_p[x] = P(x, y - 1)
    last_p: List[float] = [0.0] * (n + 1)
    # p_all[n - 1] = P(n, n)
    p_all: List[float] = [0.0] * n
    
    for y in range(1, n + 1):
        p[0] = 1.0
        for x in range(1, n + 1):
            prob_white = float(x) * float(x) / (float(x + y) * float(x + y))
            p[x] = prob_white * p[x - 1] + (1.0 - prob_white) * last_p[x]
        p_all[y - 1] = p[y]
        p, last_p = last_p, p
    
    return p_all

from matplotlib import pyplot as plt

N = 20
ps = calc_prob_by_dp_all(N)
ns = list(range(1, N + 1))
plt.plot(ns, ps)
plt.xlabel('n')
plt.xticks([1, 5, 10, 15, 20])
plt.ylabel('P(n,n)')
plt.show()

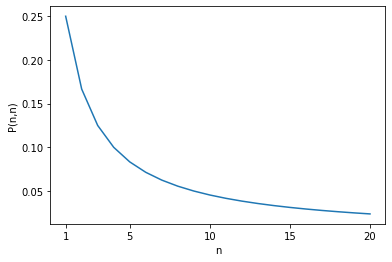
结果分析

图像看起来是符合预期的。而且所求概率随着$n$的增大大约是反比例衰减的。

我们注意到：

$$\begin{array}{rlrl}P(1)& =\frac{1}{4}& P(2)& \approx \frac{1}{6}\\ P(3)& \approx \frac{1}{8}& P(4)& \approx \frac{1}{10}\\ P(5)& \approx \frac{1}{12}& P(10)& \approx \frac{1}{22}\\ P(100)& \approx \frac{1}{202}& & \end{array}$$

嗯……看起来:

$$P(n,n)=\frac{1}{2n+2}$$

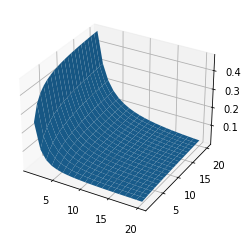
可是只猜到了$P(n,n)$的表达式，是无法完成证明的。要想通过递推式证明这个表达式，需要先得到任意的$P(x,y)$的表达式。我们最好还是画一下图、列一下数据看看。

# 用动态规划计算 P(x, y)
def calc_prob_by_dp_all_xy(n: int) -> List[List[float]]:
    # p[y][x] = P(x, y)
    p: List[List[float]] = [[0.0] * (n + 1) for _ in range(n + 1)]
    
    for y in range(1, n + 1):
        p[y][0] = 1.0
        for x in range(1, n + 1):
            prob_white = float(x) * float(x) / (float(x + y) * float(x + y))
            p[y][x] = prob_white * p[y][x - 1] + (1.0 - prob_white) * p[y - 1][x]
    
    return p

import numpy as np

N = 20
p = calc_prob_by_dp_all_xy(N)
x, y = np.meshgrid(np.arange(1, N + 1), np.arange(1, N + 1))
axes = plt.axes(projection='3d')
axes.plot_surface(x, y, np.array([p[y + 1][1:] for y in range(N)]))
plt.show()
plt.figure()
ps = [p[n][n] for n in ns]
plt.plot(ns, ps)
plt.xlabel('n')
plt.xticks([1, 5, 10, 15, 20])
plt.ylabel('P(n,n)')
plt.show()

import pandas as pd
pd.DataFrame(np.array(p)[:-1,:-1])

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
0	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
1	1.0	0.250000	0.111111	0.062500	0.040000	0.027778	0.020408	0.015625	0.012346	0.010000	0.008264	0.006944	0.005917	0.005102	0.004444	0.003906	0.003460	0.003086	0.002770	0.002500
2	1.0	0.333333	0.166667	0.100000	0.066667	0.047619	0.035714	0.027778	0.022222	0.018182	0.015152	0.012821	0.010989	0.009524	0.008333	0.007353	0.006536	0.005848	0.005263	0.004762
3	1.0	0.375000	0.200000	0.125000	0.085714	0.062500	0.047619	0.037500	0.030303	0.025000	0.020979	0.017857	0.015385	0.013393	0.011765	0.010417	0.009288	0.008333	0.007519	0.006818
4	1.0	0.400000	0.222222	0.142857	0.100000	0.074074	0.057143	0.045455	0.037037	0.030769	0.025974	0.022222	0.019231	0.016807	0.014815	0.013158	0.011765	0.010582	0.009569	0.008696
5	1.0	0.416667	0.238095	0.156250	0.111111	0.083333	0.064935	0.052083	0.042735	0.035714	0.030303	0.026042	0.022624	0.019841	0.017544	0.015625	0.014006	0.012626	0.011442	0.010417
6	1.0	0.428571	0.250000	0.166667	0.120000	0.090909	0.071429	0.057692	0.047619	0.040000	0.034091	0.029412	0.025641	0.022556	0.020000	0.017857	0.016043	0.014493	0.013158	0.012000
7	1.0	0.437500	0.259259	0.175000	0.127273	0.097222	0.076923	0.062500	0.051852	0.043750	0.037433	0.032407	0.028340	0.025000	0.022222	0.019886	0.017903	0.016204	0.014737	0.013462
8	1.0	0.444444	0.266667	0.181818	0.133333	0.102564	0.081633	0.066667	0.055556	0.047059	0.040404	0.035088	0.030769	0.027211	0.024242	0.021739	0.019608	0.017778	0.016194	0.014815
9	1.0	0.450000	0.272727	0.187500	0.138462	0.107143	0.085714	0.070312	0.058824	0.050000	0.043062	0.037500	0.032967	0.029221	0.026087	0.023438	0.021176	0.019231	0.017544	0.016071
10	1.0	0.454545	0.277778	0.192308	0.142857	0.111111	0.089286	0.073529	0.061728	0.052632	0.045455	0.039683	0.034965	0.031056	0.027778	0.025000	0.022624	0.020576	0.018797	0.017241
11	1.0	0.458333	0.282051	0.196429	0.146667	0.114583	0.092437	0.076389	0.064327	0.055000	0.047619	0.041667	0.036789	0.032738	0.029333	0.026442	0.023965	0.021825	0.019964	0.018333
12	1.0	0.461538	0.285714	0.200000	0.150000	0.117647	0.095238	0.078947	0.066667	0.057143	0.049587	0.043478	0.038462	0.034286	0.030769	0.027778	0.025210	0.022989	0.021053	0.019355
13	1.0	0.464286	0.288889	0.203125	0.152941	0.120370	0.097744	0.081250	0.068783	0.059091	0.051383	0.045139	0.040000	0.035714	0.032099	0.029018	0.026369	0.024074	0.022071	0.020313
14	1.0	0.466667	0.291667	0.205882	0.155556	0.122807	0.100000	0.083333	0.070707	0.060870	0.053030	0.046667	0.041420	0.037037	0.033333	0.030172	0.027451	0.025090	0.023026	0.021212
15	1.0	0.468750	0.294118	0.208333	0.157895	0.125000	0.102041	0.085227	0.072464	0.062500	0.054545	0.048077	0.042735	0.038265	0.034483	0.031250	0.028463	0.026042	0.023923	0.022059
16	1.0	0.470588	0.296296	0.210526	0.160000	0.126984	0.103896	0.086957	0.074074	0.064000	0.055944	0.049383	0.043956	0.039409	0.035556	0.032258	0.029412	0.026936	0.024768	0.022857
17	1.0	0.472222	0.298246	0.212500	0.161905	0.128788	0.105590	0.088542	0.075556	0.065385	0.057239	0.050595	0.045093	0.040476	0.036559	0.033203	0.030303	0.027778	0.025564	0.023611
18	1.0	0.473684	0.300000	0.214286	0.163636	0.130435	0.107143	0.090000	0.076923	0.066667	0.058442	0.051724	0.046154	0.041475	0.037500	0.034091	0.031142	0.028571	0.026316	0.024324
19	1.0	0.475000	0.301587	0.215909	0.165217	0.131944	0.108571	0.091346	0.078189	0.067857	0.059561	0.052778	0.047146	0.042411	0.038384	0.034926	0.031933	0.029321	0.027027	0.025000

结果再分析

嗯……看起来：

$$\begin{array}{rl}P(x,1)& =\frac{1}{(x+1{)}^2}\\ P(x,2)& =\frac{2}{(x+1)(x+2)}\\ P(x,3)& =\frac{3}{(x+1)(x+3)}\\ ...& \end{array}$$

也许我们有：

$$P(x,y)=\frac{y}{(x+1)(x+y)}$$

这个猜得对不对呢？我们验证一下。首先它确实满足我们之前的猜测$P(n,n)=\frac{1}{2n+2}$。

接下来我们验证它完全正确。首先关于边界条件，有：

$$\begin{array}{rl}P(x,0)& =\frac{0}{x(x+1)}=0\\ P(0,y)& =\frac{y}{y}=1\end{array}$$

结果不错。然后是递推式：

$$\begin{array}{rl}P(x,y)& =\frac{x^2}{(x+y{)}^2}\cdot P(x-1,y)+\frac{2xy+y^2}{(x+y{)}^2}\cdot P(x,y-1)\\ & =\frac{x^2}{(x+y{)}^2}\cdot \frac{y}{x(x+y-1)}+\frac{2xy+y^2}{(x+y{)}^2}\cdot \frac{y-1}{(x+1)(x+y-1)}\\ & =\frac{xy(x+1)}{(x+y{)}^2(x+1)(x+y-1)}+\frac{(2xy+y^2)(y-1)}{(x+y{)}^2(x+1)(x+y-1)}\\ & =\frac{x^{2}y+xy+2x{y}^2+y^3-2xy-y^2}{(x+y{)}^2(x+1)(x+y-1)}\\ & =\frac{y(x^2+x+2xy+y^2-2x-y)}{(x+y{)}^2(x+1)(x+y-1)}\\ & =\frac{y((x+y{)}^2-(x+y))}{(x+y{)}^2(x+1)(x+y-1)}\\ & =\frac{y((x+y)(x+y-1))}{(x+y{)}^2(x+1)(x+y-1)}\\ & =\frac{y}{(x+1)(x+y)}\end{array}$$

OHHHHHHH

太棒了，所以初始有$x$颗白色豆子和$y$颗黑色豆子时，最后一颗是黑色的概率是：

$$P(x,y)=\frac{y}{(x+1)(x+y)}$$

对于题目所说的初始时黑色豆子和白色豆子相同（均为$n$）的条件下，最后一颗是黑色的概率是：

$$P(n,n)=\frac{1}{2n+2}$$